Topics
This Lesson introduces our first ADT, the Stack. The topics include:
- The Stack ADT
- Using the Stack
- Implementation of the Stack ADT
- Problem solving and code development with Stack
Required Tasks
- Complete the tasks of Lab 2.
- Complete and submit Assignment 3.
Learning Outcomes
By the end of this lesson, you should be able to
- Define a Stack ADT
- Explain how a Stack can be used to solve a problem
- Use a Stack to solve problems similar to the ones mentioned in the lesson
- Implement the Stack ADT
Introduction
In this lesson, we are going to introduce the Stack ADT. First, we discuss the concept of a Stack, how it works, what its interface is, and how it could be used for solving a problem. Then we get into the code and see how we can develop and use a Stack in Python.
The Stack ADT
The Stack ADT represents a Last-In-First-Out (LIFO) structure. Data items are added (pushed) on top of the stack and removed (popped) from the top of the stack meaning that the last item added to the stack is always the first item removed from the stack. (Think of a stack of dishes or of cafeteria trays). The bottom is the first item that was added, the top is the last item that was added.
Created by David Brown. Used with permission.
Stack Methods
The basic stack methods are:
-
initialize() - creates an empty stack
-
push(value) -
adds
valueonto the top of the stack -
pop() - removes and returns the value on the top of the stack, if one exists
-
peek() - returns a copy of the value at the top of the stack without removing it, if one exists
-
is_empty() - returns True if the Stack is empty, False otherwise
Any implementation of a stack must define at least these methods.
The Stack ADT also contains an iterator that allows us to write code that walks through the contents of the Stack from top to bottom. We usually use this iterator for debugging purposes. It's not a method in the same sense that the methods just listed are, but it does allow us access to every value in the stack with a loop. We will demonstrate how this works later in this lesson.
The Stack Maze
Solving a Maze Using a Stack
In this section, we are going to see how we can use a stack to solve a maze. Maze is a simple game where you have an entrance to a maze and you want to find your way through it until you get to an exit. There may be side doors and corridors that you may get lost in.
The following is an example of a fairly simple maze. There is an entrance, there is an exit (at the location marked as X), and there are a number of different ways that you could travel through it, but there is only one way to actually exit the maze: at point X. Once we are at A, the points that are connected to A are B and C. We cannot go directly from A to D without going through C first. When we are at F, we can go to G or H. When we are in E, we can go to C or X.
In this sample maze, the letters represent either a decision point or an end point. We can't tell what the letter represents until we visit the point. X represents the exit point.
Input:
A simple maze, similar to the one shown in the above figure. Once we start traversing this maze, the next point is A.
Output:
A path from entrance (at the location start) to the exit (at the location X).
Example:
In the above figure, a solution is: ACEX
Another solution is: ABCDEFGHX
Solution to the maze problem
First, let's look at the figure above to see how we can find the path from start to X. Then we provide the algorithm.
To find the path from start to exit, we can start and go to the next point (A). Once at A, we may decide to go to B or C. As you see, if we choose B, we hit the wall and we need to go back to A (backtrack) and choose another location (which is C in this case). If we end up over location H, then you have to backtrack to location F.
Backtracking is an important algorithmic concept: When we make a wrong decision at a point in the maze, we need to be able to return to, not necessarily, the beginning (start) because perhaps we have gone through parts of the maze that we don't have to go through again. For example, if we go to H, we don't want to go back to start but we want to go back to F.
The point of backtracking is to return to an earlier position in the maze so that we can make a different choice. If I chose B the first time that I am at A, and that did not work, then maybe I better choose C.
This is where a stack comes in. When we are at a point (say A), we need to save all the possible points that we can go from A so that if one point does not work, we can go back and choose the next point. If we go to B and hit the wall, we should know where to come back (backtrack).
Here is the algorithm we use to solve this problem.
- Repeat steps 1 and 2 until the exit is found.
- Move to a letter point and push the immediately connected letter points, if any, from that point onto the stack. (Ignore points already visited).
- When you then need to make a decision as to where to go next, pop a point from the stack and move to that point.
The above solution to the maze finds the solution if there is one. It doesn't guarantee to find the shortest solution, it guarantees to find a solution.
Operation of the Algorithm
Let's run the algorithm on the example maze shown above and see how it gets us from the start to the exit.
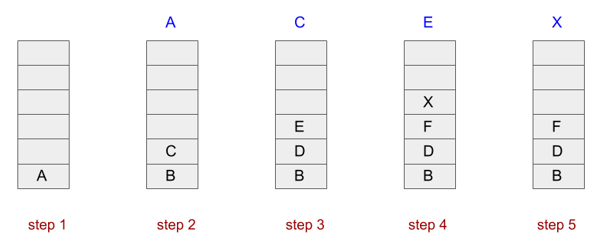
The resulting stack for this solution follows. Once a letter is popped from the stack, it is written on top of it.
Created by Masoomeh Rudafshani. Used with Permission
- We move to the start point and push on the stack all of the possible locations we can go from start. The only point available is A, so we push A onto the stack (step 1 in the above Figure).
- To decide where to go, we pop a point from the stack and move to
that point. So we pop the top of the stack and go to A (step 2). When
we get to A, we push onto the stack any point that we can see from A
(which are B and C). So, we go and push B followed by C. C ends up at
the top of the stack as the stack has the LIFO property (step 2).
When we are at a location and there is more than one letter to push ( more than one possible location), we are going to push the letters in alphabetical order. We have to have some kind of order and we arbitrarily decide on alphabetical order. If instead of letters, we had used numbers to represent location, we could push them onto stack in numeric order. It just happens to be using letters here. - To decide where to go from A, we pop a point from the stack, we get
C. So, we have gone from A to C (step 2 to step 3).
Once we pop C, we push onto the stack all the locations we can go from C, which are D and E. B still is at the bottom of the stack (step 3). - Next, we pop E. From E we can go either to F or X. So, we push F and X onto the Stack (step 4).
- Next we pop X and we are done (step 5). There are still points left on the stack, but that just means we haven't visited every possible location in the maze, which is fine. Our goal is to find the exit, not exhaustively traverse the maze.
As discussed above, we can go to the exit by going through this path: ACEX. We did not get sidetracked by B, D, or H. That was a byproduct of choosing to push the location onto the stack in alphabetical order.
The Stack Brackets
Balanced Brackets
Given an algebraic expression, determine whether the brackets (round, square, curly) are properly balanced in the expression or not. By balanced we mean that each left bracket can be matched to a corresponding right bracket so that the expression is a legitimate algebraic expression that could be evaluated.
Input:
- A mathematical expression
Output:
- True (if the brackets are balanced), False (otherwise)
Example
In the following examples, the first expression has balanced brackets while the second one does not have balanced brackets:
- \({a × 2 - [(c - d) × 4]} × sin(x - y)\)
- \(\{a × 2 - [(c - d) × 4\}]\)
Algorithm to Solve the Problem
Stacks can be used to check if brackets (round, square, curly) are properly balanced in algebraic expressions. In other words, stacks could be used to see if we have equal number of brackets and if they are in proper location.
The problem can be solved with the following algorithm:
- Initialize a stack.
- Traverse the expression one character at a time (walk through the
expression from left to right)
- If we see a left bracket of any kind, push it onto the stack.
- If we see a right bracket of any kind, pop the top of the stack and see if it is the left complement to the right bracket.
- The brackets are not balanced if one of the following is true:
- An item popped from the stack does not match the corresponding right bracket.
- We encounter a right bracket, but the stack is empty.
- We reach the end of the expression but the stack is not empty.
Trying the Algorithm
Try the algorithm for yourself. Enter a string into the Expression box, and use to process the expression, and to try another one:
Try the following expressions to see what the algorithm does:
- a string with balanced brackets
- a string with no brackets
- a string with too many left brackets
- a string with too many right brackets
- a string with mismatched brackets
The Array-Based Stack
There are a number of different approaches to implementing ADTs. These implementations vary depending on the programming language used, and the capabilities of these languages. We will use two different implementation styles: array-based and linked. We will begin with an array-based stack and work with linked structures later in the course.
Implementing the Array-Based Stack
Many programming languages have built-in array data types. An array is an area of memory that holds a series of consecutive data elements, with each data element accessible through an index value. Arrays are of fixed length. Python does not have a array data type built-in to its basic language set. A Python list is closest thing available, but such lists are not of fixed length, nor do they require that all their elements be of the same type. However, we will treat Python lists as though they are arrays for two reasons: the array concept is extremely important in other languages; and it is easier to call a list data structure written in Python an array-based list as opposed to a list-based list.
Thus our first implementation of the Stack ADT uses a Python list, named
_values as the underlying means of storing the Stack's
data. We will wrap the Python list code with our own in order
to meet our ADT standards.
The top of the stack is the right-most inhabited element in the stack's array. As data is pushed onto the top of the stack, the index of the right-most inhabited element increases; as elements are removed, the index of the right-most inhabited element decreases. The size of the stack at any given time is simply the number of array elements in the Python list. No array elements with an index smaller than that of the right-most element can be left empty. A stack is empty if the underlying Python list is empty.
This figure displays the workings of the array-based Stack. Use and to see how it works:
Initializing
The ADTs are implemented with Python classes. So, we define a class
named Stack. The class has a Python list attribute named _values
which stores data items.
from copy import deepcopy
class Stack:
def __init__(self):
"""
-------------------------------------------------------
Initializes an empty stack. Data is stored in a Python list.
Use: stack = Stack()
-------------------------------------------------------
Returns:
a new Stack object (Stack)
-------------------------------------------------------
"""
self._values = []
As noted earlier __init__ is a Python magic method name,
and a Stack should never be created by calling __init__
directly. The
Use: stack = Stack()
shows how
the constructor should be called.
Note the naming convention used here. The attribute names start with an
underscore '_' which indicates that no program that uses
the Stack should ever refer to these attributes directly. These
attributes are to be treated as private attributes that are
available only to the stack itself. Any and all attempts to access or
modify the Stack must be done through the public methods of the
class. Public methods are those methods whose names do not start with an
underscore such as push method discussed next.
The reference to deepcopy is discussed in a later section.
The push Method
Adding data to the stack is called pushing. The push method is very similar to how append method in an Array-based List ADT is implemented (look at previous lesson for more details). We need to insert the data item at the end of the Array and increase the value of top.
push
def push(self, value):
"""
-------------------------------------------------------
Pushes a copy of value onto the top of the stack.
Use: stack.push(value)
-------------------------------------------------------
Parameters:
value - value to be added to stack (?)
Returns:
None
-------------------------------------------------------
"""
self._values.append(deepcopy(value))
return
push simply uses the Python list method append
to add value to the end of the _values list.
Using deepcopy
Note the use of the deepcopy method, and the related import
in Code Listing 1. copy is a Python library, and deepcopy
is one of its methods. deepcopy returns a complete copy of
whatever is passed to it. (Using the copy library requires
an from copy import deepcopy statement at the top of the
module, as you can see in Code Listing 1.) It is important to understand
what happens if we don't use it. The following code shows the creation
of two Student objects:
Student Objects
s1 = Student("123456789", "Brown", "David", "1962-10-25")
s2 = s1
print("Student 1:")
print(s1)
print()
print("Student 2:")
print(s2)
and the (unsurprising) output:
Student 1: 123456789 Brown, David M, 1962-10-25 Student 2: 123456789 Brown, David M, 1962-10-25
Now let's update the contents of one of (or so we think) the Student
objects:
Student Objects
s1.student_id = "999999999"
s1.forename = "Tasmin"
s1.birth_date = "2000-01-01"
print("Student 1:")
print(s1)
print()
print("Student 2:")
print(s2)
and the (perhaps surprising) output:
Student 1: 999999999 Brown, Tasmin 2000-01-01 Student 2: 999999999 Brown, Tasmin 2000-01-01
This demonstrates that the s2 Student object is a reference
to s1 Student object, not a copy of it. To make
sure we get a copy, we need to explicitly tell Python to make a copy. We
could write code to do so, but Python provides a deepcopy
method to do exactly this. Now if we write:
deepcopying a Student Object
s1 = Student("123456789", "Brown", "David", "1962-10-25")
s2 = deepcopy(s1)
s1.student_id = "999999999"
s1.forename = "Tasmin"
s1.birth_date = "2000-01-01"
print("Student 1:")
print(s1)
print()
print("Student 2:")
print(s2)
we get:
Student 1: 999999999 Brown, Tasmin 2000-01-01 Student 2: 123456789 Brown, David 1962-10-25
which is more what we had in mind.
Thus, when we add values to a data structure, whatever it is, (in this
example pushing onto a Stack), we want to make sure the data structure
has a value independent of anything outside of it. Using deepcopy
makes a copy of an object in the stack, so that the original object and
the object in the data structure point to different memory locations, as
in this diagram:
deepcopy
As we can see, there are now two copies of the student data, and changes
to one can in no way affect the other. We will use deepcopy
often within our ADT implementations. It must be used whenever we are
putting data into the structure or allowing external programs to examine
that data. It is not needed when removing data from a data structure
because the data structure doesn't care what happens to data once that
data is removed from it.
The following diagram shows Python Tutor graphically displaying how various objects are stored in memory:
deepcopy
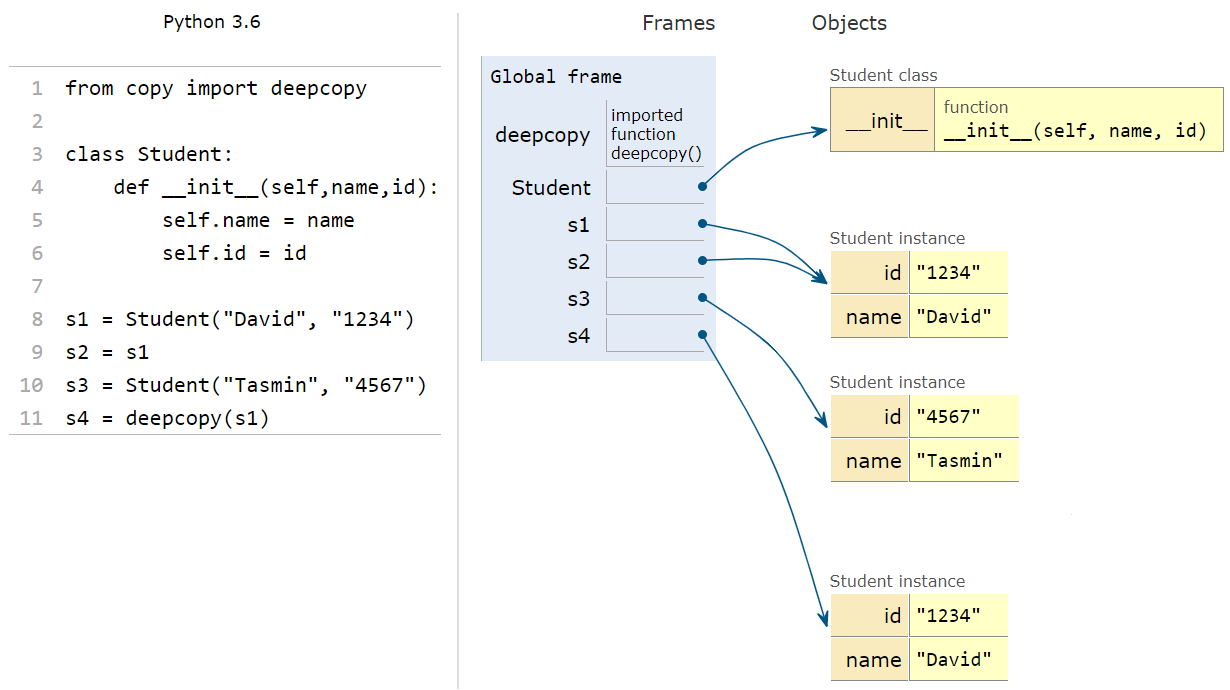
The objects s1 and s2 point to the same
location in memory because s2 was defined as a reference to
s1. s3 is an entirely new object and occupies
its own location in memory. s4, as a deepcopy
of s1, also occupies its own location in memory. s1
and s4 contain the same values, but are not the same
objects.
The Stack Mirror
Mirror problem (coding)
In this section we are going to see how we can use a stack to solve the Mirror problem. First, we define the problem, then we discuss how the stack can be used to solve this problem, and finally we develop the code. The code is developed gradually in several steps. The code developed here uses Stack ADT methods. Note that it doesn't matter what the underlying implementation of the Stack class actually is, the Mirror solution calls only the publicly available methods.
Problem Definition
Given a string and a mirror character, we want to determine if the string is a mirror. A string is a mirror if it has the mirror character in the middle and the left and right sides of the mirror character are in the reverse order to one another; i.e., the left portion of the string has the same characters as the right portion of the string but they are in the reverse order. A mirror string has the general form:
LmR
where:
mis the mirror character at the centre of the stringLandRare strings whereRis the reverse ofL(They may be empty strings)LandRare formed from a limited set of characters that do not includem
Example:
Assume "m" is the mirror character, and the valid character set is any of "abc". The following strings are mirror strings:
- abcmcba
- abmba
while the following are not mirror strings:
- abcmcb
- gmg (g is not a valid character from the character set)
- abcmab
- amz
Solution Algorithm
We are going to use a stack to solve this problem. A stack is used to store the contents of the left side L of the (potential) mirror string. We can then compare it against the right side L to see if they are the complement of each other or not. A Stack is useful here because we push characters onto the stack in order, but retrieve them in reverse order.
Coding the Solution
In this section, we are going to write the code. We want to write a function that takes a string as input and determines whether the string is a mirror or not. The mirror character and alphabet are maintained as constants in the program. We will develop this function step by step and mention how a stack can help us in solving this problem and writing the code. We are going to develop and test the following function:
Step 1
is_mirror Definition
from Stack_array import Stack
MIRROR = "m"
CHARS = "abc"
def is_mirror(string):
"""
-------------------------------------------------------
Determines if string is a mirror of characters in valid_chars around the pivot
MIRROR. A mirror is of the form LmR, where L is the reverse of R, and L and R
contain only characters in CHARS.
Use: mirror = is_mirror_stack(string)
-------------------------------------------------------
Parameters:
string - the string to test (str)
Returns:
mirror - True if string is a mirror, False otherwise (boolean)
-------------------------------------------------------
"""
Step 2
def is_mirror(string):
mirror = True
stack = Stack()
n = len(string)
i = 0
while i < n and string[i] != MIRROR:
# Debugging line:
print(f" i: {i}, string[i]: {string[i]}")
i += 1
return mirror
We assume that a given string is a mirror until discovered otherwise.
That's why we set mirror to be True on line 2
in the above listing.
We are going to use a stack to solve this problem. The stack is
implemented in the Stack_array module and we need to import it
(line 1 in Code Listing 1). We also need to initialize a variable of
type Stack (line 3). We need to walk through the left side
of the string. So, we need a loop to go through all the characters until
we either hit the end of the string or find the mirror character m.
Step 3
In the previous step, we read the left half of the string L.
Now, we want to compare its contents against the right side of the
string R, but we have to do so in reverse order. To achieve
that goal we must push every character in L onto a stack.
is_mirror with Stack push
def is_mirror(string):
mirror = True
stack = Stack()
n = len(string)
i = 0
while i < n and string[i] != MIRROR:
# Debugging line:
print(f" i: {i}, string[i]: {string[i]}")
stack.push(string[i])
i += 1
# Debugging using Stack iterator:
print("The contents of the stack:")
for value in stack:
print(value)
return mirror
To see that stack contains the characters in L in reverse,
we print the contents of the stack after we read L. As
noted earlier, the Stack ADT contains an iterator that allows us to
print the content of the Stack as if it were a Python list. We use a for
loop to walk through the elements in the Stack and print them, as shown
in lines 15-16 above. These are the results if we use the string "abc"
as the parameter:
i: 0, string[i]: a i: 1, string[i]: b i: 2, string[i]: c The contents of the stack: c b a
Step 4
We now want to compare the contents of the stack against the right side
of the string R. Therefore, we go through the remainder of
the string and corresponding to each character we pop a character from
the stack. Because of the LIFO property of the stack, we retrieve the
left side in reverse order. The following code does this:
is_mirror with Stack pop
mirror = True
stack = Stack()
n = len(string)
i = 0
while i < n and string[i] != MIRROR:
stack.push(string[i])
i += 1
while mirror and i < n and not stack.is_empty():
c = stack.pop()
# Debugging line:
print(f" i: {i}, string[i]: {string[i]}, c: {c}")
if string[i] != c:
mirror = False
else:
i += 1
return mirror
We cannot peek or pop when the stack is empty. That's why we need to
make sure that stack is not empty as done in line 10 by calling the is_empty()
method on stack. Also, if the character just read does not
match the one on top of the stack, there is no point in continuing, so
we conclude that the string is not a mirror. So we set mirror
to False which results in stopping the loop in line 10. You
do not need to explicitly use mirror == True in the loop
conditions, just using the value of mirror directly as a
condition is sufficient.
Step 5
To fix the problem mentioned in the previous step we need to skip over the mirror character found by the first loop, because that was the character being processed when the second loop starts:
is_mirror Skipping Over mirror Character
def is_mirror(string):
mirror = True
stack = Stack()
n = len(string)
i = 0
while i < n and string[i] != MIRROR:
stack.push(string[i])
i += 1
# skip over the mirror character
i += 1
while mirror and i < n and not stack.is_empty():
c = stack.pop()
if string[i] != c:
mirror = False
else:
i += 1
return mirror
The string "abcmcba" should now cause the function to return True.
Step 6
is_mirror Checking State of Stack and i
def is_mirror(string):
mirror = True
stack = Stack()
n = len(string)
i = 0
while i < n and string[i] != MIRROR:
stack.push(string[i])
i += 1
# skip over the mirror character
i += 1
while mirror and i < n and not stack.is_empty():
c = stack.pop()
if string[i] != c:
mirror = False
else:
i += 1
# check final conditions
if not (i == n and stack.is_empty()):
mirror = False
return mirror
In the above code, on line 23, we added the final condition to check
whether the end of the string parameter is reached at the same time the
stack is empty. This implies that there are no characters remaining in R
to compare, and all of the characters in L and R
compared so far match. The string "abcm" violates this because although
we reached the end of the string, stack is not empty.
Step 7
is_mirror Checking for Valid Characters
def is_mirror(string):
mirror = True
stack = Stack()
n = len(string)
i = 0
# check mirror to avoid infinite loop (why?)
while mirror and i < n and string[i] != MIRROR:
if string[i] in CHARS:
stack.push(string[i])
i += 1
else:
mirror = False
# skip over the mirror character
i += 1
while mirror and i < n and not stack.is_empty():
c = stack.pop()
if string[i] != c:
mirror = False
else:
i += 1
# check final conditions
if not (i == n and stack.is_empty()):
mirror = False
return mirror
When checking a string we do not care what's on the right side R
if the left side L contains an invalid character. So, we
add the condition on line 8 in the above code. Now the code is complete
generates the correct return values for all of the following string
parameters:
- "abmcba":
False - "abba":
False - "abmba":
True - "azmza":
False - "m":
True
Stack Applications
Other than the examples already given, stacks have a number of uses in computer science.
Balancing Symbols
One of the main use of Stack is to check balancing symbols. We showed how this algorithm work in section 3.4 where we talked about balanced brackets. This technique is used in compilers to check programs for syntax errors.
Expression Evaluation
Stacks are also a very useful tool for evaluating arithmetic expressions. We are used to writing arithmetic expression with infix notation, where operators are between operands and parentheses are used to enforce precedence:
\(1+2\times 3+(4\times 5-6)\times 7\)
However, it is faster to evaluate an arithmetic expression written in postfix notation where the operators follow the operands and no parentheses are needed as long as each operator has a fixed number of operands:
\(1\ 2\ 3\times +\ 4\ 5\times 6 - 7\times +\)
Stacks could be used for both evaluating a postfix expression and also converting an infix expression to a postfix expression.
Postfix Expressions
A postfix expression can be evaluated using the following algorithm:
- Walk through the expression
- When you see a operand, push it onto the stack
- When you see an operator, pop two operands from the stack, apply
the operator on the two operands. The first operand popped appears
on the right of the operation and the second operand popped
appears on the left of the operation. e.g.:
pop 6, pop 7, pop -: 7 - 6
Push the result back onto the stack.
The following shows how the sample postfix expression can be evaluated using a Stack:
| Step | Expression |
|---|---|
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + | |
| 1 2 3 * + 4 5 * 6 - 7 * + |
| Step | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Operation | * | + | * | - | * | + | ||||
| Stack | ||||||||||
| 3 | 5 | 6 | 7 | |||||||
| 2 | 6 | 4 | 20 | 20 | 14 | 14 | 98 | |||
| 1 | 1 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 105 |
As we walk through the expression each symbol encountered and the changes on the Stack due to each symbol is shown in red.
Modified from Masoomeh Rudafshani. Used with Permission
Note that these are very simplified expressions - an operand may consist of multiple digits and negative numbers.
Infix to Postfix Conversion
Stacks can also be used to convert an expression in infix form into postfix. We provide the algorithm in the following. Here we assume that the only operators in the expression are +, *, (, and ) where parenthesis has the highest precedence and + has the lowest precedence.
Algorithm to Convert Infix to Postfix
- Start with an empty stack.
- Traverse the entire expression.
- When you see an operand, place it onto the output.
- When you see a left parentheses place it onto stack.
- When you see a right parenthesis, then pop the stack until you see a matching left parenthesis, which is popped as well. All the popped items are written to the output except the left parenthesis.
- When you see any other symbol ('+','*', '(' ), then pop entries from the stack until you find an entry of lower priority. All the popped items are written to the output. Exception: you should never remove a '(' from the stack except when processing a ')'.
- When you read the end of the expression, pop the stack until it is empty, and write the popped symbols onto the output.
The following figure shows the execution of the algorithm on the expression \(a+b*c+(d*e+f)*g\) to convert it to postfix notation. As we walk though the expression, each symbol read is shown in blue and the changes on output and stacks are in shown in red. In step 6, when we read a '+', we pop '*' and '+' from the Stack and write them to the output. The reason is that '*' has a higher precedence and '+' has the same precedence. The '+' on the Stack is the one just read. It is similar to step 11, where we read a '+', we need to pop all the items until we find an entry of lower priority. We pop '*' and write it to output, as shown in step 11. However, we don't pop ')' as mentioned in the exception part in the algorithm. In step 13, we see a right parenthesis and remove all the items from the Stack and write them to the output, except for the parenthesis. In step 14, we place '*' on top of the stack as there is not operand with lower priority on the Stack.
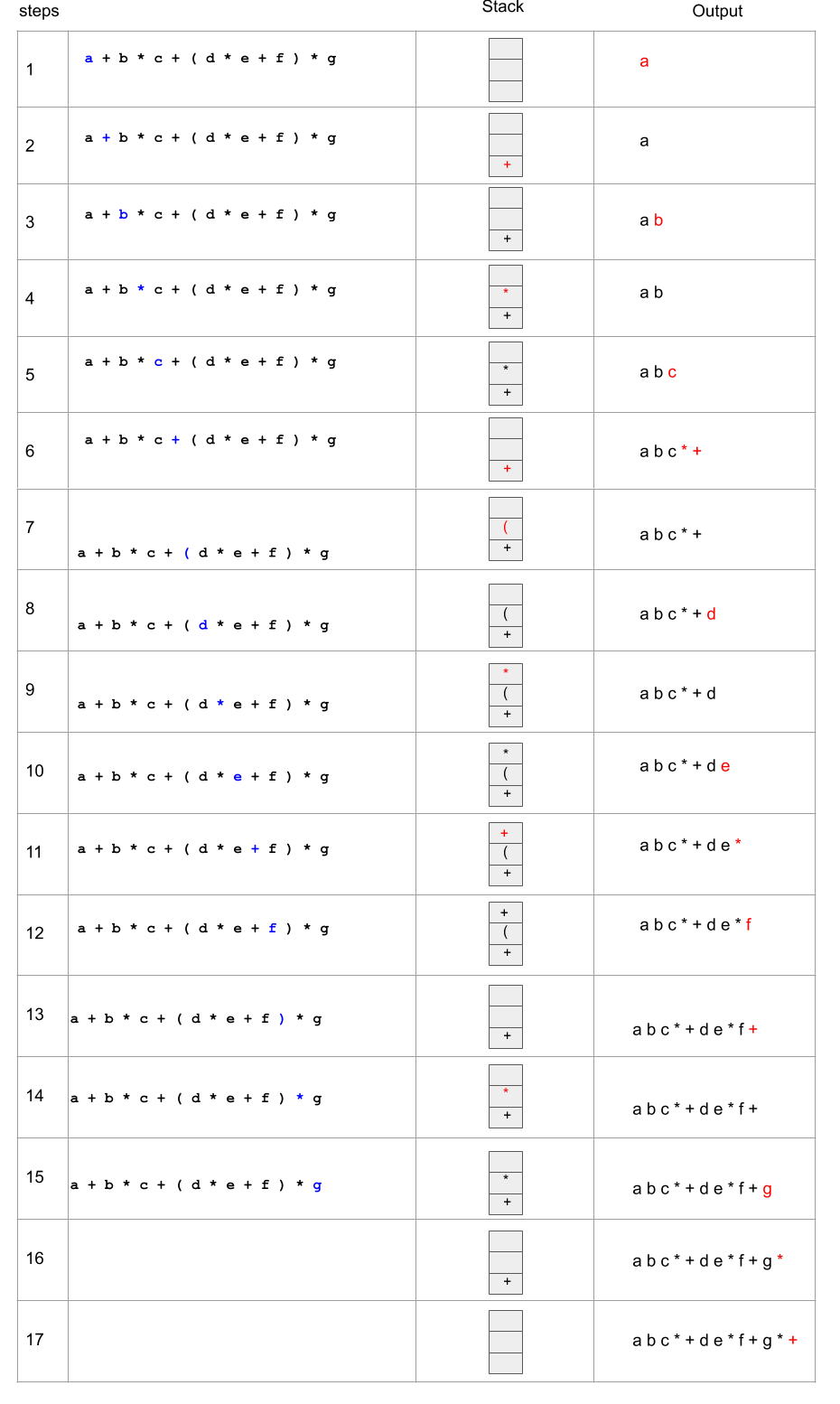
As we walk through the expression, each symbol encountered is turned blue. The changes on the Stack and output due to each read symbol is shown in red.
Created by Masoomeh Rudafshani. Used with Permission.
Summary
In this lesson we introduced the Stack ADT. You can think of a stack as a list where the items can be entered and removed from only one side of the list. We discussed how a Stack can be implemented using Python lists and how Stacks can be used to solve problems. Later we in the course we will talk about another implementation of the Stack ADT using a linked structure.
References
- Data Structures and Algorithm Analysis in C++, Mark Allen Weiss. 2006.