The CPUlator: https://cpulator.01xz.net/?sys=arm-de1soc.
Recursion
In the Stack Frames lab we learned how to use stack frames when defining subroutines. As a useful side benefit the use of stack frames allows subroutines to be re-entrant. If code can be interrupted, but is returned to the same state as it was when interrupted, and then can resume executing as if it was never interrupted, that code is re-entrant. Recursive code works this way: a subroutine makes a call to itself and is able to continue execution without bad side-effects after the completion of the recursive call. Stack frames make the implementation of recursion easy.
The gcd subroutine uses recursion to find the Greatest
Common Denominator of two positive integers. Its algorithm is (roughly)
the equivalent of the following C code (Euclid's algorithm):
int gcd(a, b) {
if(a == b) {
return a;
} else if(a > b) {
return gcd(b, a - b);
} else {
return gcd(b, a);
}
The entire program is available at gcd_recursive.s.
The main program call to gcd is:
gcd Call
ldr r1, =numbers // get address of numbers
ldr r2, [r1, #4] // put second number into register (4 bytes past first number)
stmfd sp!, {r2} // push second number onto stack
ldr r2, [r1] // put first number into register
stmfd sp!, {r2} // push first number onto stack
bl gcd // call the subroutine
add sp, sp, #8 // release the parameter memory from the stack
// Result in r0
str r0, [r1, #8] // write result back to memory (8 bytes past first number)
Note that the source of the numbers is arbitrary - in this example we
get the numbers from memory. Although the numbers come from memory, they
are passed by value - i.e. as the actual numbers, not the memory
addresses of the numbers - to the gcd subroutine, and the result is
returned in r0.
The subroutine then creates a stack frame and extracts the parameters from that stack frame:
gcd Stack Frame and Parameters
stmfd sp!, {fp} // preserve frame pointer
mov fp, sp // save current stack top to frame pointer
// preserve other registers including lr because of recursive call
stmfd sp!, {r1, lr}
// Copy parameters into registers
ldr r0, [fp, #4] // get a
ldr r1, [fp, #8] // get b
The main body of the subroutine follows the given algorithm in defining
the recursive base case (a ==
b) making the recursive call when the base case is not true. In making
the recursive call the subroutine pushes a new set of parameters onto
the stack and a new stack frame is created:
gcd Recursive Call
cmp r0, r1
beq _gcd // a is the gcd: return in r0
subgt r0, r0, r1 // a > b: gcd(b, a - b)
// else: gcd(b, a)
stmfd sp!, {r0} // 2nd parameter - push a onto the stack
stmfd sp!, {r1} // 1st parameter - push b onto the stack
bl gcd // recursive call to subroutine
When each call to the subroutine ends the subroutine has to clean up its own stack frame:
gcd Stack Frame Clean Up
add sp, sp, #8 // release parameter memory from stack
_gcd:
ldmfd sp!, {r1, lr} // pop preserved registers
ldmfd sp!, {fp} // pop frame pointer
bx lr // return from subroutine
Other than the fact the the subroutine is recursive, and therefore the lr
register must be preserved between calls or the subroutine will lose the
to return to when it ends, there is nothing different about how it
handles stack frames than in any of our previous examples.
After the main call to gcd and two recursive calls the stack contains:
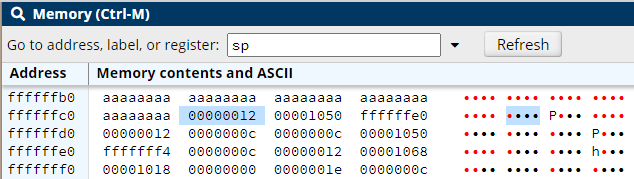
which is more easily readable as:
| Address | Value | Comment |
|---|---|---|
| ffffffc4 | 00000012 | // preserve r1 |
| ffffffc8 | 00001050 | // preserve lr |
| ffffffcc | ffffffe0 | // frame pointer |
| ffffffd0 | 00000012 | // 1st parameter |
| ffffffd4 | 0000000c | // 2nd parameter |
| 2nd recursive call ↑ | ||
| ffffffd8 | 0000000c | // preserve r1 |
| ffffffdc | 00001050 | // preserve lr |
| ffffffe0 | fffffff4 | // frame pointer |
| ffffffe4 | 0000000c | // 1st parameter |
| ffffffe8 | 00000012 | // 2nd parameter |
| 1st recursive call ↑ | ||
| ffffffec | 00001068 | // preserve r1 |
| fffffff0 | 00001018 | // preserve lr |
| fffffff4 | 00000000 | // frame pointer |
| fffffff8 | 0000001e | // 1st parameter |
| fffffffc | 0000000c | // 2nd parameter |
| main subroutine call ↑ | ||
| 100000000 | ||
We are seeing recursion 'under the hood', so to speak. This example
shows how re-entrant code works, the basic idea being that once a
routine call has finished, the state of the registers must be identical
to what they were before the routine was called, except for any return
value (usually returned in r0). The routines may also
update memory if that's their purpose. When the gcd
subroutine finishes only the r0 register has not been
preserved as what it was before the subroutine was called.
The following dynamic diagram shows how the stack frame for this program is handled:
Blue line is code to be executed
Red items are the changed items
| Register | Value |
|---|---|
| r0 | 00000000 |
| r1 | 00000000 |
| r2 | 00000000 |
| r11 (fp) | 00000000 |
| r12 (ip) | 00000000 |
| r13 (sp) | 100000000 |
| r14 (lr) | 00000000 |
| r15 (pc) | 00000000 |
| Address | Code | Comment |
|---|---|---|
| 00001000 | ldr r1, =numbers |
// get address of numbers |
| 00001004 | ldr r2, [r1, #4] |
// put second number into register |
| 00001007 | stmfd sp!, {r2} |
// push second number onto stack |
| 0000100C | ldr r2, [r1] |
// put first number into register |
| 00001010 | stmfd sp!, {r2} |
// push first number onto stack |
| 00001014 | bl gcd |
// call the subroutine |
| 00001018 | add sp, sp, #8 |
// release parameter memory |
| _stop: | ||
| 00001020 | b _stop |
// end program |
| gcd: | ||
| 00001024 | stmfd sp!, {fp} |
// preserve frame pointer |
| 00001028 | mov fp, sp |
// save stack top to frame pointer |
| 0000102c | stmfd sp!, {r1, lr} |
// preserve temporary registers |
| 00001030 | ... | // gcd code |
| 00001044 | stmfd sp!, {r0} |
// 2nd parameter - push a |
| 00001048 | stmfd sp!, {r1} |
// 1st parameter - push b |
| 0000104c | bl gcd |
// recursive call |
| 00001050 | add sp, sp, #8 |
// release parameter memory |
| _gcd: | ||
| 00001054 | ldmfd sp!, {r1, lr} |
// pop preserved registers |
| 00001058 | ldmfd sp!, {fp} |
// pop frame pointer |
| 0000105c | bx lr |
// return from subroutine |
| numbers: | ||
| 00001068 | 18 (Ox00000012) | |
| 0000106c | 12 (Ox0000000c) | |
| 00001070 | 0 | |
| Address | Value | Comment |
|---|---|---|
| 100000000 | ||
-
The file l07_t01.s contains the following subroutine:
isUpperCase: /* ------------------------------------------------------- Determines if a character is an upper case letter. ------------------------------------------------------- Parameters r2 - character to test Returns: r0 - returns True (1) if upper case, False (0) otherwise ------------------------------------------------------- */ mov r0, #0 // default False cmp r2, #'A' blt _isUpperCase // less than 'A', return False cmp r2, #'Z' movle r0, #1 // less than or equal to 'Z', return True _isUpperCase: bx lrThis subroutine does not use the stack to preserve any registers because it is using
r2as the source of its data and not changing it, and is returning its result inr0. It returns to the line after it is called withbx lr, which copies the contents of the link register back to the program counter.The file also contains the subroutine
isLowerCase, which works the same way. Type a character into the UART and run the program to see what happens.The file also contains the subroutine
isLetter, which uses theisLowerCaseandisUpperCasesubroutines to determine if a character is a letter or not://------------------------------------------------------- isLetter: /* ------------------------------------------------------- Determines if a character is a letter. ------------------------------------------------------- Parameters r2 - character to test Returns: r0 - returns True (1) if letter, False (0) otherwise ------------------------------------------------------- */ bl isLowerCase // test for lowercase cmp r0, #0 bleq isUpperCase // not lowercase? Test for uppercase. bx lrThis looks like the previous subroutines, yet this subroutine fails in an interesting way. Uncomment the call to it, run the program, and explain how it fails and correct the problem. You must retain the subroutine calls to
isLowerCaseandisUpperCase.Add your comments to the location where you corrected the code and surround your comments and code with the following comments:
//======================================================= // comments and corrected code //=======================================================
-
The file l07_t02.s contains the following subroutine definition:
Palindrome: /* ------------------------------------------------------- Determines if a string is a palindrome. ------------------------------------------------------- Parameters r4 - address of first character of string to test r5 - address of last character of string to test Uses: R? - ? Returns: r0 - returns True (1) if palindrome, False (0) otherwise ------------------------------------------------------- */Complete this subroutine with a recursive algorithm. (Fix the problem in
isLetteras you did for the previous task.)- the string contains only lower case letters, no digits, spaces, or punctuation (ex: "otto")
- string has mixed case, but only letters (ex: "RaceCar")
- string has mixed case, and non-letters (ex: "A man, a plan, a canal, Panama!")
All versions must return false for a non-palindrome (ex: "David"). Do not change the contents of the string in memory.
Hint: here is Python code for a recursive palindrome function:
def palindrome(string): if len(string) <= 1: pal = True elif not string[0].isalpha(): pal = is_pal(string[1:]) elif not string[-1].isalpha(): pal = is_pal(string[:-1]) elif string[0].lower() != string[-1].lower(): pal = False else: pal = is_pal(string[1:-1]) return pal
Zip your files together in zip file named login_l07.zip (using your Laurier login, of course) and submit that zip file to the MLS dropbox.