2 C Features - Pointers and Arrays

2.4 Array data structures for applications

There are four major reasons why arrays are used to represent and store data in applications.

1. Data records to be presented have the same type.
2. The maximum number of data records is known.
3. There are many random access operations in the applications.
4. Data elements have a regular relationship like vector, table, and matrix.

For example, char arrays are used to store strings. A string is a sequence of characters. We will introduce the concepts of strings in Lesson 3. Arrays are used to implement other linear data structures like queues and stacks, in which data records are organized in a linear order. We will look into array queues and stacks in Lesson 7. 1D arrays are used to implement mathematical vectors, 2D arrays are used to implement matrices and rectangular tables. In computer graphics, 2D arrays are used to represent transformation matrix.

2.4.1 Using arrays in applications

Since an array is declared with data type and maximum length, we need to know the type of data records and the max number of data records that the application can possibly have, so as to create an array to store application data.

Using an array to store a collection of application data records, we often insert a new data record into the array, and delete an existing data record from the array. For the efficiency of insert and delete operations, it is better to put data records in consecutive positions of the array, and use two variables to store the start and end positions of data records in the array. For example, we use variables right to represent the index of the last data record and left to represent the index of the first data record in the array, set left = right = -1 when there is no data, and keep 0 <= left <= right <= MAX-1, where MAX is the length of the array.

Example:

#define MAX 10
int a[MAX], left, right;
a[2] = 6;
a[3] = 5;
a[4] = 4;
left = 2;
right = 4;

Figure 1 shows the diagram of the above array example.

The following are the basic array data structure operations.

1. Traverse – access/visit every data record in the array
2. Search – find a data record in the array by a key value
3. Insert – add a new data record in the array
4. Delete – remove a data record from the array
5. Sort – rearrange data records in ascending or descending order

Next we look into these operations. Assume that we are given an array data structure: int a[MAX], left, right;.

Traverse

Traversing the array can be done by using a for loop. For example, we can do traversal and printing as follows.

void display(int a[], int left, int right) {
  int i;
  for( i = left; i <= right; i++) {
    printf("%d ", a[i]);
  }
}

Search

Searching by a key means finding the position of an element that matches the key value. It returns the position if found; otherwise returns -1.

A simple searching algorithm is to traverse the array with key checking and return when found. Following function is a simple implementation of the simple searching algorithm.

int search(int a[], int left, int right, int key) {
  for( i = left; i <= right; i++) 
    if (a[i] == key) return i;  // found, return the position
  return -1;                    // not found
} 

Insert

Inserting an element into an array means adding the new data record into the array at a specific position. The position can be:

1. at the beginning, i.e., before the first data record.
2. before a data record of a specific key value.
3. at the end, i.e. after the last data record.
4. after an element of a specific key value.

For example, Figure 2 shows the diagram of inserting a value at the beginning.

Figure 3 shows the diagram of inserting a value after a specific key value.

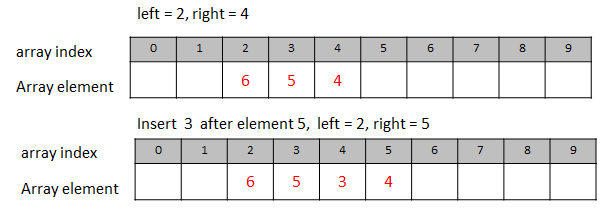
Let’s look into the case of inserting at the beginning. There are multiple solutions/algorithms, the following one is a better one due to the time efficiency.

Algorithm: insert at the beginning
Step 1: If left = -1, then put new data record at position 0, and set left=right=0
Step 2: If left > 0, then put new element at position left-1, and set left = left -1
Step 3: else if right = MAX-1, print OVERFLOW, goto step 6.
Step 4: else (left = 0, right < MAX), shift all data records back one position
Step 5: put the new data record at position 0, reset right = right + 1.
Step 6: stop, output left and right

We see that in Step 2, the insertion does not shift data, so it takes less time in this case.

To implement the above algorithm by a function, it needs to pass the references of left and right to the function as parameters because after the insertion, the values of left and right may be changed. The following function is an implementation of the algorithm.

int insert_beg(int a[], int *left_ptr, int *right_ptr, int data) {
  int left = *left_ptr; 
  if (left == -1) {    // no data in the array
    a[0] = data;
    *left_ptr = 0;
    *right_ptr = 0;
  }
  else if (left > 0) {  // if there is a room before the position of the first element. 
    a[left-1] = data;
    *left_ptr = left-1;
  }
  else {
    int right = *right_ptr; 
    
    // no room to insert
    if (right == MAX-1) { 
      printf("overflow");
      return 0; // indicate that the insertion fails
    }
    
    // shift every element back one position
    int i;
    for (i = right; i >= left; i--) { 
       a[i+1] = a[i];  
    }
    a[left] = data;
    *right_ptr = right+1;
  }
  return 1; // indicate that the insertion is successful 
} 

Stop and think

Think about the algorithms and implementations of inserting before a specific positions. How do you use this operation to build a sorted array in increasing order?

Delete

Deleting an element from an array means removing a data record at a specific position. The position can be specified as:

1. at the beginning, i.e., delete the first data record
2. at the end, i.e., delete the last data record
3. a data record of a specific key value, i.e., delete record(s) matched with a given key value

Deleting the first element can be done by setting left = left + 1 if left < right; and setting left = right = -1 if left == right.

Stop and think

The algorithms of deleting a data record of specific key value.

Sort

Sorting an array is to rearrange the array elements in ascending or descending order of key values of data elements.

Why do we want to sort an array? With sorted arrays, operations like searching, finding median, and computing percentile can be done efficiently.

The sorting problem is one of well-studied problems in Computer Science. There are many sorting algorithms, in this course we will look into several sorting algorithms from perspective of data structures. Let’s start from the simple selection sort algorithm (supplementary link).

To do the selection sort in a function, we can pass the input data array to the function, keep the sorted array in the same array. That is, after the function call, the input array becomes sorted array. This kind of sorting is called in-place sorting.

The following program contains two implementations of the selection sort algorithm. One uses array index, another uses pointers.

#include <stdio.h>
void display_array(int *, int, int);
void selection_sort(int *, int, int);
void selection_sort_pointer(int *, int, int);

int main(){
  int a[10] = {5, 9, 0, 8, 7, 4, 6, 3, 2, 1};
  display_array(a, 0, 9);
  selection_sort(a, 0, 9);
  //selection_sort_pointer(a, 0, 9);
  display_array(a, 0, 9);
  return 0;
}
void display_array(int *p, int left, int right) {
  int *ptr = p+left;
  int *max = p+right;
  while (ptr<max)
    printf("%d ", *ptr++);
  printf("\n");
}
void selection_sort(int x[], int left, int right) {  // use subscripts to access array elements
  int i, j, k, t;
  for (i = left; i <= right; i++) {
    k = i;
    for (j = i + 1; j <= right; j++)
      if (x[j] < x[k]) 
        k = j;
    if (k != i) { // swap
      t = x[i];
      x[i] = x[k]; 
      x[k] = t;  
    }
  }
}
void selection_sort_pointer(int *x, int left, int right) { // use pointers to access array elements
  int i, j, k, t;
  for (i = left; i<=right; i++){
    k = i;
    for (j = i + 1; j <= right; j++)
       if (*(x+j) < *(x+k)) 
         k = j;
    
    if (k != i){ // swap
      t = *(x+i); 
      *(x+i) = *(x+k);
      *(x+k) = t; 
    }
  }
}
/* output:
5 9 0 8 7 4 6 3 2 1
0 1 2 3 4 5 6 7 8 9

Sometimes, an application that only needs a sorted result, e.g. find the median, does not want to change the input array data structure. In such a situation, an array of pointers can be used to point to data records in the array data structure. Then, do the sorting on the array of pointers using the key values of the data elements pointed by the pointers. The following program example shows such an application.

#include <stdio.h>
void display_array(int*, int, int);
void display_array_pointer(int**, int, int);
void selection_sort_array_pointer(int**, int, int);

int main(){
  int a[10] = {5, 9, 0, 8, 7, 4, 6, 3, 2, 1};
  int *pa[10];  //pointer array to hold addresses of int data elements
  int i;
  for (i=0; i<10; i++) {
     pa[i] = &a[i]; // let pa[i] hold the address of a[i]
  }
  printf("Original data array\n");
  display_array(a, 0, 9); 
  
  printf("Pointer array before sorting\n");  
  display_array_pointer(pa, 0, 9);
  
  selection_sort_array_pointer(pa, 0, 9);
  
  printf("Pointer array after sorting\n");
  display_array_pointer(pa, 0, 9);
  
  printf("Original data array\n");
  display_array(a, 0, 9);  

  return 0;
}
void display_array(int *p, int left, int right) {
  int *ptr = p+left;
  int *max = p+right;
  while (ptr<max)
    printf("%d ", *ptr++);
  printf("\n");
}
void display_array_pointer(int **p, int left, int right) {
  int **ptr = p+left;
  int **max = p+right;
  while (ptr<max)
    printf("%d ", *(*ptr++));
  printf("\n");
}
//sort pointer array using pointed data in comparison
void selection_sort_array_pointer(int **x, int left, int right) { 
  int i, j, k, *t;
  for (i = left; i <= right; i++){
    k = i;
    for (j = i + 1; j <= right; j++)
       if (**(x+j) < **(x+k)) 
         k = j;
    
    if (k != i){ // swap
      t = *(x+i); 
      *(x+i) = *(x+k);
      *(x+k) = t; 
    }
  }
}
/*
Original data array
5 9 0 8 7 4 6 3 2
Pointer array before sorting
5 9 0 8 7 4 6 3 2
Pointer array after sorting
0 1 2 3 4 5 6 7 8
Original data array
5 9 0 8 7 4 6 3 2
*/

2.4.2 Summary

You learned the fundamental array data structures for applications. The drawback of the arrays is that the length of an array is fixed once it is instanced. As a result, it causes overflow when the number of data records is bigger than the length. It wastes spaces when the number of data records is much less than the length.

Stop and think

1. Can you find a method to get around the drawback of arrays? Namely, what can be done if an overflow happens and what can be done when number of data records is much less than the length?

2. How do you sort a subset of an application data records? For example, the given application data are a group of integers stored in an array, you are to sort the subset of even numbers of the group and find the median of the even numbers.

2.4.3 Exercises

Self-quiz

Take a moment to review what you have read above. When you feel ready, take this self-quiz which does not count towards your grade but will help you to gauge your learning. Answer the questions posed below.

Go back