| Maximum Needs | Allocate | Need | Available | |
|---|---|---|---|---|
| T0 | 10 | 5 | 5 | 3 |
| T1 | 4 | 2 | 2 | |
| T2 | 9 | 2 | 7 |
Deadlocks
Introduction to Deadlock
- In a multiprogramming environment, multiple threads compete for limited resources.
- A thread requests resources; if unavailable, it waits.
- Sometimes, a waiting thread can never proceed because the resources it needs are held by other waiting threads, leading to a deadlock.
- Deadlock occurs when every process in a set is waiting for an event that only another process in the set can cause.
- Chapter Objectives:
- Describe deadlocks that prevent concurrent processes from completing tasks.
- Present methods to prevent or avoid deadlocks in a computer system.
System Model
- A system has a finite number of resources distributed among competing threads.
- Resources are partitioned into types, each with identical instances (e.g., CPU cycles, files, I/O devices).
- For example, four CPUs mean the CPU resource type has four instances.
- Mutex locks and semaphores are common system resources and frequent sources of deadlock.
- If a thread requests an instance of a resource type, the allocation of any instance of the type should satisfy the request. If it does not, then the instances are not identical, and the resource type classes have not been defined properly. Therefore:
- Resource types: \(R_1, R_2, \ldots, R_m\) (e.g., CPU cycles, memory space, I/O devices)
- Each resource type \(R_i\) has \(W_i\) instances.
- The number of resources requested may not exceed the total number of resources available in the system.
System Model
- Each process utilizes a resource as follows:
- Request: The thread requests the resource. If the request cannot be granted immediately then the requesting thread must wait until it can acquire the resource.
- Use: The thread can operate on the resource (for example, if the resource is a mutex lock, the thread can access its critical section).
- Release: The thread releases the resource.
- The request and release of resources may be system calls, examples are the request() and release() of a device
- allocate() and free() memory system calls.
- wait() and signal() operations on semaphores and through acquire() and release() of a mutex lock.
System Model
- A system table records whether each resource is free or allocated. For each allocated resource, the table also records the thread to which it is allocated.
- If a thread requests a resource currently allocated to another thread, it can be added to a queue of threads waiting for this resource.
- To illustrate a deadlocked state, consider the dining-philosophers problem:
- Resources are represented by chopsticks.
- If all philosophers get hungry simultaneously and each grabs the chopstick on their left, no chopsticks are available.
- Each philosopher is then blocked, waiting for their right chopstick to become available.
- Developers of multithreaded applications must remain aware of the possibility of deadlocks.
Deadlock in Multithreaded Applications
/* thread_one runs in this function */
void * do_work_one (void *param)
{
pthread_mutex_lock (& first_mutex );
pthread_mutex_lock (& second_mutex );
/** * Do some work */
pthread_mutex_unlock (& second_mutex );
pthread_mutex_unlock (& first_mutex ); pthread_exit (0);
} /* thread_two runs in this function */
void * do_work_two (void *param)
{
pthread_mutex_lock (& second_mutex );
pthread_mutex_lock (& first_mutex );
/*** Do some work */
pthread_mutex_unlock (& first_mutex );
pthread_mutex_unlock (& second_mutex );
pthread_exit (0);
}Deadlock in Multithreaded Applications
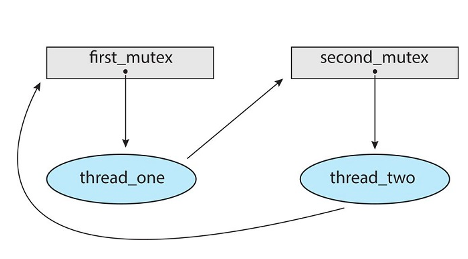
thread_oneattempts to acquire the mutex locks in the order (1) first_mutex , (2) second_mutex.- At the same time,
thread_twoattempts to acquire the mutex locks in the order (1)second_mutex, (2)first_mutex. - Deadlock is possible if thread_one acquires
first_mutexwhilethread_twoacquiressecond_mutex. - Note that, even though deadlock is possible, it will not occur if thread_one can acquire and release the mutex locks for
first_mutexandsecond_mutexbeforethread_twoattempts to acquire the locks. - And, of course, the order in which the threads run depends on how they are scheduled by the CPU scheduler.
- It is difficult to identify and test for deadlocks that may occur only under certain scheduling circumstances.
Livelock
- Livelock is another form of liveness failure.
- It is similar to deadlock; both prevent two or more threads from proceeding, but the threads are unable to proceed for different reasons.
- Whereas deadlock occurs when every thread in a set is blocked waiting for an event that can be caused only by another thread in the set, livelock occurs when a thread continuously attempts an action that fails.
- `pthreads pthread_mutex_trylock() function, which attempts to acquire a mutex lock without blocking.
- This situation can lead to livelock if
thread_oneacquiresfirst_mutex, followed bythread_twoacquiringsecond_mutex. - Each thread then invokes
pthread_mutex_trylock(), which fails, releases their respective locks, and repeats the same actions indefinitely. - It thus can generally be avoided by having each thread retry the failing operation at random times.
Livelock
/* thread_one runs in this function */
void * do_work_one (void *param)
{
int done = 0; while (!done) {
pthread_mutex_lock (& first_mutex );
if ( pthread_mutex_trylock (& second_mutex ))
{/*** Do some work */ pthread_mutex_unlock (& second_mutex );
pthread_mutex_unlock (& first_mutex );
done =_1;}
else
pthread_mutex_unlock (& first_mutex );}
pthread_exit (0);
}
/* thread_two runs in this function */
void * do_work_two (void *param)
{
int done = 0;
while (!done)
{
pthread_mutex_lock (& second_mutex );
if ( pthread_mutex_trylock (& first_mutex ))
{
/*** Do some work*/
pthread_mutex_unlock (& first_mutex );
pthread_mutex_unlock (& second_mutex );
done =_1;
}
else
pthread_mutex_unlock (& second_mutex );
}
pthread_exit (0);
}Deadlock Characterization
Deadlock can arise if four conditions hold simultaneously.
Mutual exclusion: only one process at a time can use a resourceHold and wait: a process holding at least one resource is waiting to acquire additional resources held by other processesNo preemption: a resource can be released only voluntarily by the process holding it, after that process has completed its taskCircular wait: there exists a set \(\{P_0, P_1, \ldots, P_n\}\) of waiting processes such that \(P_0\) is waiting for a resource that is held by \(P_1\), \(P_1\) is waiting for a resource that is held by \(P_2\), \(\ldots\), \(P_{n-1}\) is waiting for a resource that is held by \(P_n\), and \(P_n\) is waiting for a resource that is held by \(P_0\).All four conditions must hold for a deadlock to occur. The circular-wait condition implies the hold-and-wait condition, so the four conditions are not completely independent
Resource-Allocation Graph
- Deadlocks can be described more precisely in terms of directed graph called a system resource-allocation graph.
- Graph is a set of vertices V and a set of edges E .
- V is partitioned into two types:
- T = {\(T_1\) , \(T_2\) , …, \(T_n\) }, the set consisting of all the active threads in the system
- R = \({ R_1 , R_2 , …, R_m }\), the set consisting of all resource types in the system.
- Each thread \(T_i\) is represented as a circle and each resource type \(R_j\) as a rectangle.
- request edge – directed edge \(T_i \rightarrow R_j\)
- assignment edge – directed edge \(R_j \rightarrow T_i\)
Resource-Allocation Graph (Cont.)

Resource-Allocation Graph (Cont.)
- Figure represents the deadlock situation.
- Resource type \(R_j\) may have more than one instance, each such instance is represented as a dot within the rectangle.
- Note that a request edge points only to the rectangle \(R_j\) , whereas an assignment edge must also designate one of the dots in the rectangle.
- When thread \(T_i\) requests an instance of resource type \(R_j\) , a request edge is inserted in the resource-allocation graph.
- When this request can be fulfilled, the request edge is instantaneously transformed to an assignment edge.
- When the thread no longer needs access to the resource, it releases the resource. As a result, the assignment edge is deleted.
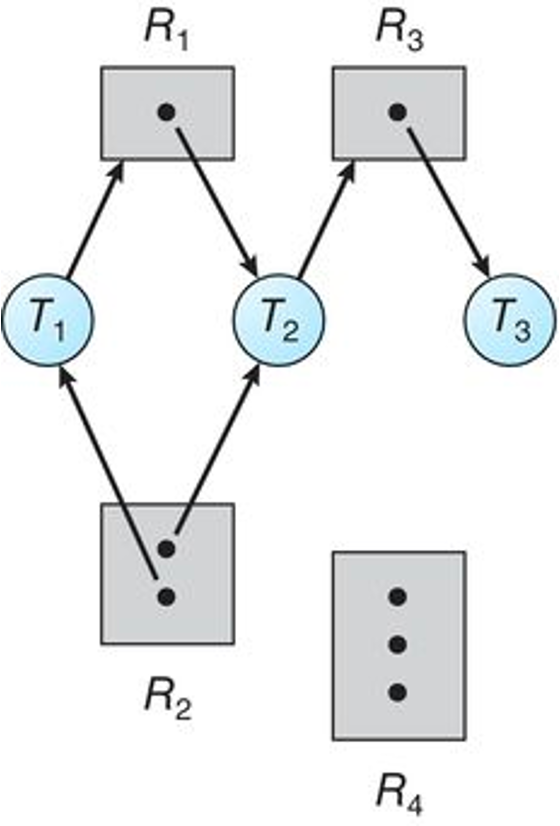
Example of a Resource Allocation Graph
- The resource-allocation graph depicts the following situation.
- The sets T , R , and E :
- T = { \(T_1\) , \(T_2\) , \(T_3\) }
- \(R = { R_1 , R_2 , R_3 , R_4 }\)
- E = {\(T_1\) \(\rightarrow\) \(R_1\) , \(T_2\) \(\rightarrow\) \(R_3\), \(R_1\) \(\rightarrow\) \(T_2\) , \(R_2\) \(\rightarrow\) \(T_2\) , \(R_2\) \(\rightarrow\) \(T_1\) , \(R_3\) \(\rightarrow\) \(T_3\) }
- Resource instances:
- One instance of resource type \(R_1\)
- Two instances of resource type \(R_2\)
- One instance of resource type \(R_3\)
- Three instances of resource type \(R_4\)
- Thread states:
- Thread \(T_1\) is holding an instance of resource type \(R_2\) and is waiting for an instance of resource type \(R_1\).
- Thread \(T_2\) is holding an instance of \(R_1\) and an instance of \(R_2\) and is waiting for an instance of \(R_3\).
- Thread \(T_3\) is holding an instance of \(R_3\).
Example of a Resource Allocation Graph
- Given the definition of a resource-allocation graph, it can be shown that, if the graph contains no cycles, then no thread in the system is deadlocked.
- If the graph does contain a cycle, then a deadlock may exist.
- If each resource type has exactly one instance, then a cycle implies that a deadlock has occurred.
- If the cycle involves only a set of resource types, each of which has only a single instance, then a deadlock has occurred.
- Each thread involved in the cycle is deadlocked. In this case, a cycle in the graph is both a necessary and a sufficient condition for the existence of deadlock.
- If each resource type has several instances, then a cycle does not necessarily imply that a deadlock has occurred. In this case, a cycle in the graph is a necessary but not a sufficient condition for the existence of deadlock.

Resource Allocation Graph With A Deadlock
- Suppose that thread \(T_3\) requests an instance of resource type \(R_2\). Since no resource instance is currently available, we add a request edge \(T_3 \rightarrow R_2\) to the graph.
- At this point, two minimal cycles exist in the system:
- \(T_1 \rightarrow R_1 \rightarrow T_2 \rightarrow R_3 \rightarrow T_3 \rightarrow R_2 \rightarrow T_1\)
- \(T_2 \rightarrow R_3 \rightarrow T_3 \rightarrow R_2 \rightarrow T_2\)
- Threads \(T_1\), \(T_2\), and \(T_3\) are deadlocked.
- Thread \(T_2\) is waiting for the resource \(R_3\), which is held by thread \(T_3\). Thread \(T_3\) is waiting for either thread \(T_1\) or thread \(T_2\) to release resource \(R_2\).
- In addition, thread \(T_1\) is waiting for thread \(T_2\) to release resource \(R_1\).
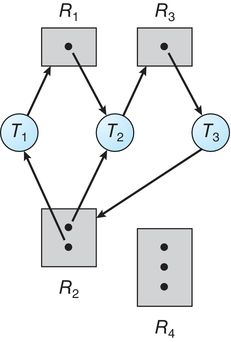
Graph With A Cycle But No Deadlock
- We also have a cycle: \(T_1\) \(\rightarrow\) \(R_1\) \(\rightarrow\) \(T_3\) \(\rightarrow\) \(R_2\) \(\rightarrow\) \(T_1\)
- However, there is no deadlock. Observe that thread \(T_4\) may release its instance of resource type \(R_2\) .
- That resource can then be allocated to \(T_3\) , breaking the cycle.
- To summarize, if a resource-allocation graph does not have a cycle, then the system is not in a deadlocked state.
- If there is a cycle, then the system may or may not be in a deadlocked state.
- This observation is important when we deal with the deadlock problem.
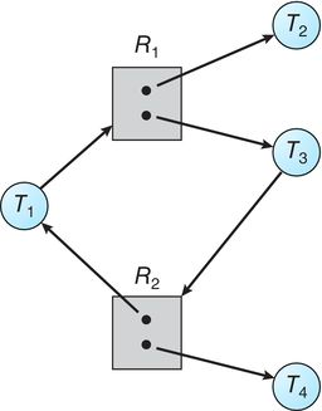
Example
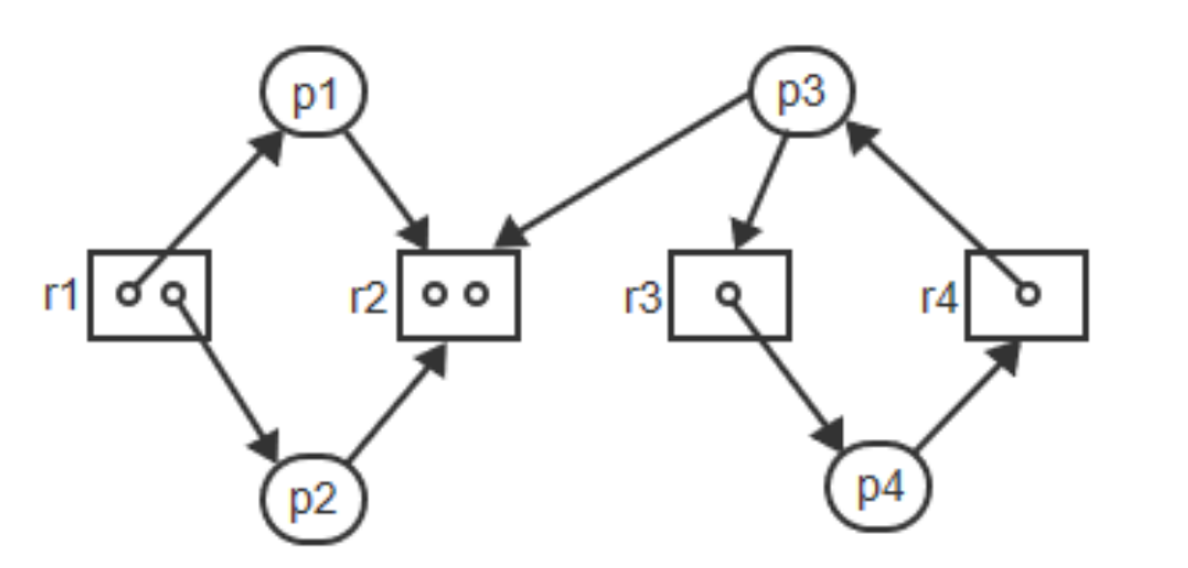
- \(p_3\) and \(p_4\) are in deadlock.
Basic Facts
- If graph contains no cycles \(\implies\) no deadlock
- If graph contains a cycle \(\implies\)
- if only one instance per resource type, then deadlock
- if several instances per resource type, possibility of deadlock
Methods for Handling Deadlocks
- We can handle deadlocks in three ways:
- Ignore the problem and pretend deadlocks never occur (used by most OS, including UNIX).
- Use a protocol to prevent or avoid deadlocks, ensuring the system never enters a deadlocked state.
- Allow the system to enter a deadlocked state, detect it, and recover.
Methods for Handling Deadlocks
- Ensure the system never enters a deadlock state:
- Deadlock prevention: Methods to ensure at least one necessary condition cannot hold.
- Deadlock avoidance: Requires advance information about resource requests and usage.
- The OS decides if a thread should wait based on:
- Currently available resources.
- Resources allocated to each thread.
- Future requests and releases of each thread.
- The OS decides if a thread should wait based on:
Deadlock Prevention
- By ensuring that at least one of these conditions cannot hold, we can prevent the occurrence of a deadlock.
- Mutual Exclusion – not required for sharable resources (e.g., read-only files); must hold for non-sharable resources; Read-only files are a good example of a sharable resource; A thread never needs to wait for a sharable resource.
- Hold and Wait – must guarantee that whenever a process requests a resource, it does not hold any other resources
- Require process to request and be allocated all its resources before it begins execution or allow process to request resources only when the process has none allocated to it.
- Low resource utilization; starvation possible
- Alternatively, if a thread requests some resources:
- We first check whether they are available. If they are, we allocate them.
- If they are not, we check whether they are allocated to some other thread that is waiting for additional resources.
- If so, we preempt the desired resources from the waiting thread and allocate them to the requesting thread.
- If the resources are neither available nor held by a waiting thread, the requesting thread must wait.
- We first check whether they are available. If they are, we allocate them.
Deadlock Prevention (Cont.)
- No Preemption – If a process that is holding some resources requests another resource that cannot be immediately allocated to it, then all resources currently being held are released
- Preempted resources are added to the list of resources for which the process is waiting
- Process will be restarted only when it can regain its old resources, as well as the new ones that it is requesting
- Using this protocol the circular-wait condition cannot hold.
- In this we assign each resource a unique integer number, which allow resources to be compared.
- Each thread can ask the resources in increasing order. Alternatively, if thread must release higher order resource before requesting lower order.
- Let the set of threads involved in the circular wait be { \(T_0\) , \(T_1\) , …, \(T_n\) }, where \(T_i\) is waiting for a resource \(R_i\) , which is held by thread \(T_{i +1}\) . Then, since thread \(T_{i +1}\) is holding resource \(R_i\) while requesting resource \(R_{i +1}\) , we must have \(F ( R_i ) < F ( R_{i +1} )\) for all \(i\).
- But this condition means that \(F ( R_0 ) < F ( R_1 ) < … < F ( R_n ) < F ( R_0 )\). By transitivity, \(F ( R_0 ) < F ( R_0 )\), which is impossible. Therefore, there can be no circular wait.
Deadlock Avoidance
- Requires additional a priori information:
- Example: System with resources \(R_1\) and \(R_2\) needs to know thread P will request \(R_1\) then \(R_2\), while thread Q will request \(R_2\) then \(R_1\).
- With this sequence knowledge, the system can decide if a thread should wait to avoid deadlock.
- Each request decision considers:
- Resources currently available.
- Resources currently allocated to each thread.
- Future requests and releases of each thread.
- Simplest model: Each process declares the maximum number of resources it may need.
- Deadlock-avoidance algorithm ensures no circular-wait condition.
- Resource-allocation state defined by:
- Number of available and allocated resources.
- Maximum demands of the processes.
Safe State
- A state is safe if the system can allocate resources to each thread (up to its maximum) in some order and still avoid a deadlock.
- When a process requests an available resource, the system must decide if immediate allocation leaves the system in a safe state.
- A sequence of threads < \(T_1\), \(T_2\), \(\ldots\), T_n > is a safe sequence for the current allocation state if, for each \(T_i\), the resource requests that \(T_i\) can still make can be satisfied by the currently available resources plus the resources held by all \(T_j\), with \(j < i\).
- If the resources that \(T_i\) needs are not immediately available, then \(T_i\) can wait until all \(T_j\) have finished. When they have finished, \(T_i\) can obtain all of its needed resources, complete its task, return its allocated resources, and terminate. When \(T_i\) terminates, \(T_{i+1}\) can obtain its needed resources, and so on.
- If no such sequence exists, then the system state is said to be unsafe.
Safe, Unsafe, Deadlock State
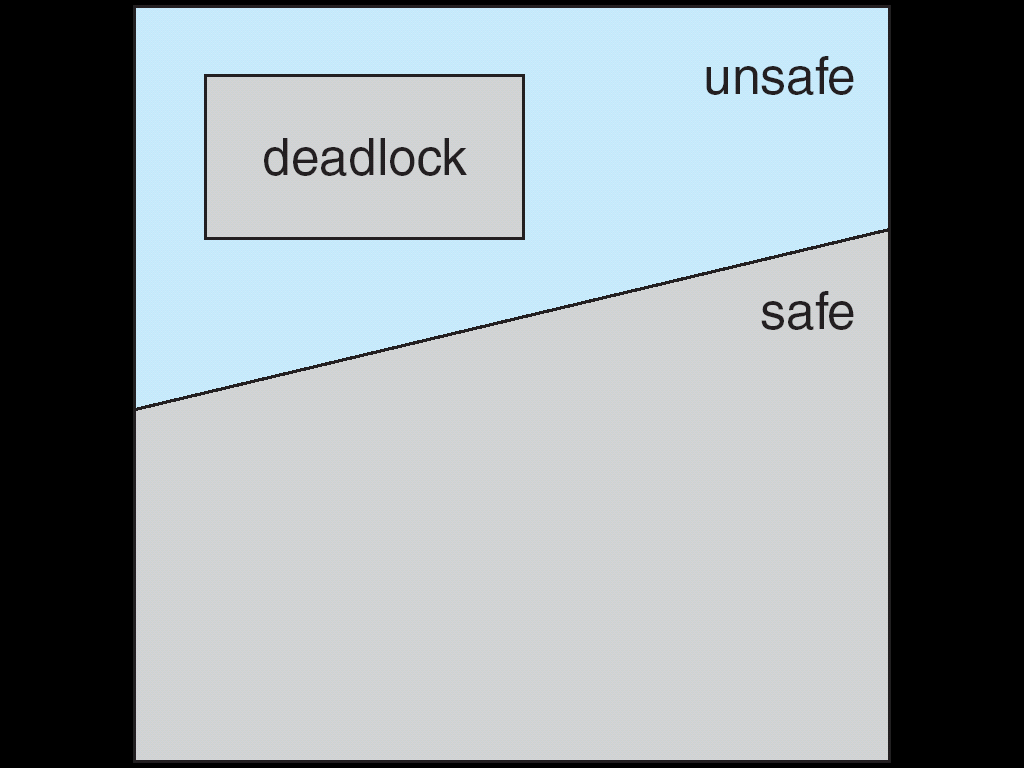
Basic Facts
- If a system is in safe state –> no deadlocks
- If a system is in unsafe state –> possibility of deadlock
- Avoidance –> ensure that a system will never enter an unsafe state.
Avoidance Algorithms
- A single instance of a resource type
- Use a resource-allocation graph
- Multiple instances of a resource type
- Use the banker’s algorithm
Example
- To illustrate, consider a system with twelve resources and three threads: \(T_0\), \(T_1\), and \(T_2\).
- Thread \(T_0\) requires ten resources, thread \(T_1\) may need as many as four, and thread \(T_2\) may need up to nine resources.
- Suppose that, at time \(t_0\), thread \(T_0\) is holding five resources, thread \(T_1\) is holding two resources, and thread \(T_2\) is holding two resources. (Thus, there are three free resources.)
Need = Max need – Allocation; \({Available}_i\) = \({Available}_{(i-1)} + Allocate\).- At time \(T_0\) , the system is in a safe state. The sequence < \(T_1\) , \(T_0\) , \(T_2\) > satisfies the safety condition.
- Thread \(T_1\) can immediately be allocated all its resources and then return them (the system will then have five available resources);
- then thread \(T_0\) can get all its resources and return them (the system will then have ten available resources);
- and finally thread \(T_2\) can get all its resources and return them (the system will then have all twelve resources available).
Example
Example
- A system can go from a safe state to an unsafe state. Suppose that, at time \(T_1\) , thread \(T_2\) requests and is allocated one more resource.
- The system is no longer in a safe state. At this point, only thread \(T_1\) can be allocated all its resources.
- When it returns them, the system will have only four available resources. Since thread \(T_0\) is allocated five resources but has a maximum of ten, it may request five more resources. If it does so, it will have to wait, because they are unavailable.
- Similarly, thread \(T_2\) may request six additional resources and have to wait, resulting in a deadlock. Our mistake was in granting the request from thread \(T_2\) for one more resource.
- If we had made \(T_2\) wait until either of the other threads had finished and released its resources, then we could have avoided the deadlock.
- The system is no longer in a safe state. At this point, only thread \(T_1\) can be allocated all its resources.
Example
| Maximum Needs | Allocate | Need | Available | |
|---|---|---|---|---|
| T0 | 10 | 5 | 5 | 2 |
| T1 | 4 | 2 | 2 | |
| T2 | 9 | 3 | 6 |
Example
- One mistake in granting the request from thread T2 for one more resource resulted in deadlock.
- We could have avoided the deadlock if we could have postponed the allocation of an additional resource to T2 until other threads have finished and released their resources.
Example
- Given the concept of a safe state, we can define avoidance algorithms that ensure that the system will never deadlock.
- The idea is simply to ensure that the system will always remain in a safe state. Initially, the system is in a safe state.
- Whenever a thread requests a resource that is currently available, the system must decide whether the resource can be allocated immediately or the thread must wait.
- The request is granted only if the allocation leaves the system in a safe state.
- In this scheme, if a thread requests a resource that is currently available, it may still have to wait. Thus, resource utilization may be lower than it would otherwise be.
Example
Total Resources = 15, Threads = 3
| Maximum Needs | Allocate | Need | Available | |
|---|---|---|---|---|
| T0$ | 6 | 3 | ||
| T1 | 7 | 5 | ||
| T2 | 8 | 4 |
Example

Resource-Allocation Graph Scheme
- A variant of resource-allocation graph with only one instance per resource type.
- Introduce a new type of edge, called a claim edge.
- A claim edge \(T_i \dashrightarrow R_j\) indicates that thread \(T_i\) may request resource \(R_j\) in the future.
- Represent claim edges by dashed lines.
- When thread \(T_i\) requests resource \(R_j\), convert the claim edge \(T_i \dashrightarrow R_j\) to a request edge.
- When resource \(R_j\) is released by \(T_i\), reconvert the assignment edge \(R_j \rightarrow T_i\) to a claim edge \(T_i \dashrightarrow R_j\).
- Resources must be claimed a priori in the system.
- Before thread \(T_i\) starts executing, all its claim edges must appear in the resource-allocation graph.
Resource-Allocation Graph Scheme
- Suppose thread \(T_i\) requests resource \(R_j\).
- The request can be granted only if converting the request edge \(T_i \rightarrow R_j\) to an assignment edge \(R_j \rightarrow T_i\) does not form a cycle in the resource-allocation graph.
- A cycle-detection algorithm, requiring \(O(n^2)\) operations (where \(n\) is the number of threads), is used.
- If no cycle exists, the allocation leaves the system in a safe state.
- If a cycle is found, the allocation puts the system in an unsafe state, and thread \(T_i\) must wait.
Resource-Allocation Graph
- Suppose that \(T_2\) requests \(R_2\).
- Although \(R_2\) is currently free, we cannot allocate it to \(T_2\) , since this action will create a cycle in the graph.
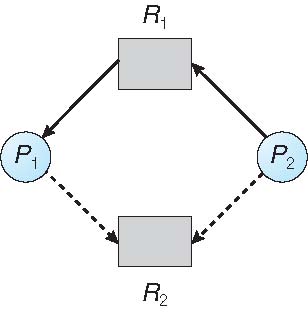
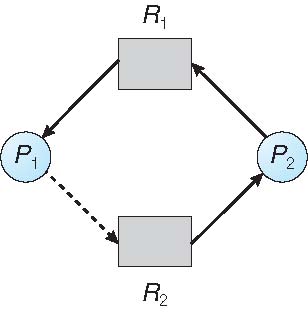
Unsafe State In Resource-Allocation Graph
- A cycle indicates that the system is in an unsafe state. If \(T_1\) requests \(R_2\), and \(T_2\) requests \(R_1\), then a deadlock will occur.
Banker’s Algorithm
- The resource-allocation-graph algorithm is not applicable to a resource-allocation system with multiple instances of each resource type.
- Banker’s algorithm can apply to Multiple instances
- When a new thread enters the system, it must declare the maximum number of instances of each resource type that it may need.
- This number may not exceed the total number of resources in the system.
- Data Structures for the Banker ’ s Algorithm
- Several data structures must be maintained to implement the banker’s algorithm.
- These data structures encode the state of the resource-allocation system.
- Let n = number of processes, and m = number of resources types.
- Available : (Vector of length (m)). If \({available}[j] = k\), there are \(k\) instances of resource type \(R_j\) available.
- Max : (n \(\times\) m matrix). If \({Max}[ i,j ] = k\), then process \(T_i\) may request at most \(k\) instances of resource type \(R_j\).
- Allocation : (n \(\times\) m matrix). If \({Allocation}[ i,j ] = k\), then \(T_i\) is currently allocated \(k\) instances of \(R_j\).
- Need : (n \(\times\) m matrix). If \({Need}[ i,j ] = k\), then \(T_i\) may need \(k\) more instances of \(R_j\) to complete its task. \({Need}[ i,j ] = \text{Max}[ i,j ] - \text{Allocation}[ i,j ]\)
- These data structures vary over time in both size and value.
Data Structures for the Banker ’s Algorithm
- Let \(X\) and \(Y\) be vectors of length n.
- We say that \(X ≤ Y\) if and only if \(X [ i ] ≤ Y [ i ]\) for all \(i =_1,_2, …, n\).
- For example, if \(X = (1,7,3,2)\) and \(Y = (0,3,2,1)\), then \(Y ≤ X\) . In addition, \(Y < X\) if \(Y ≤ X\) and \(Y ≠ X\).
- We can treat each row in the matrices Allocation and Need as vectors and refer to them as \({Allocation}_i\) and \({Need}_i\) .
- The vector \({Allocation}_i\) specifies the resources currently allocated to thread \(T_i\) ; the vector \(Need_i\) specifies the additional resources that thread \(T_i\) may still request to complete its task.
Safety Algorithm
- Let Work and Finish be vectors of length m and n , respectively. Initialize Work = Available and Finish [ i ] = false for i = 0, 1, …, n −1.
- Find an index i such that both
- \(Finish[ i ] == false\)
- \(Need_i ≤ Work\)
- If no such i exists, go to step_4.
- \(Work = Work + {Allocation}_i\)
- \(Finish [ i ] = true\) Go to step_2.
- \(Work = Work + {Allocation}_i\)
- If \(Finish [ i ] == true\) for all \(i\) , then the system is in a safe state.
- This algorithm may require an order of \(m × n^2\) operations to determine whether a state is safe.
Resource-Request Algorithm for Process \(P_i\)
- \({Request}_i\) = request vector for process \(T_i\) . If ${Request}_i [ j ] = k then process \(T_i\) wants k instances of resource type R j
- If \({Request}_i \leq {Need}_i\) go to step 2. Otherwise, raise error condition, since process has exceeded its maximum claim
- If \({Request}_i \leq {Available}\) , go to step_3. Otherwise \(T_i\) must wait, since resources are not available
- Pretend to allocate requested resources to \(T_i\) by modifying the state as follows:
- Available = Available – \({Request}_i\) ;
- \({Allocation}_i\) = \({Allocation}_i\) + \({Request}_i\) ;
- \({Need}_i\) = \({Need}_i\) – \({Request}_i\) ;
- If safe –> the resources are allocated to \(T_i\)
- If unsafe –> \(T_i\) must wait, and the old resource-allocation state is restored
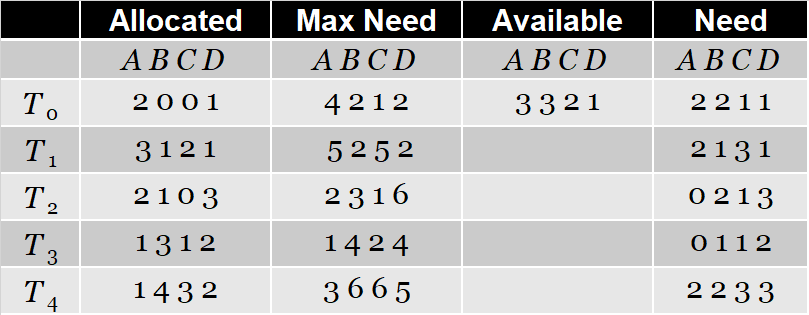
Example of Banker’ s Algorithm
5 processes \(P_0\) through \(P_4\) ;
3 resource types: A (10 instances), B (5instances), and C (7 instances)
Snapshot at specific time is given in the table:
| Allocated | Max Need | Available | Need | |
|---|---|---|---|---|
| A B C | A B C | A B C | A B C | |
| T0 | 0 1 0 | 7 5 3 | 3 3 2 | |
| T1 | 2 0 0 | 3 2 2 | ||
| T2 | 3 0 2 | 9 0 2 | ||
| T3 | 2 1 1 | 2 2 2 | ||
| T4 | 0 0 2 | 4 3 3 |
Example (Cont.)
- The content of the matrix Need is defined to be Max – Allocation
- The system is in a safe state since the sequence < \(T_1\) , \(T_3\) , \(T_4\) , \(T_2\) , \(T_0\) > satisfies safety criteria
| Need | |
|---|---|
| A B C | |
| T0 | 7 4 3 |
| T1 | 1 2 2 |
| T2 | 6 0 0 |
| T3 | 0 1 1 |
| T4 | 4 3 1 |
Example: \(T_1\) Request (1,0,2)
- Check that Request \(\leq\) Available (that is, (1,0,2) \(\leq\) (3,3,2) –> true
- Executing safety algorithm shows that sequence < \(T_1\) , \(T_3\) , \(T_4\) , \(T_0\) , \(T_2\) > satisfies safety requirement
| Allocated | Max Need | Available | Need | |
|---|---|---|---|---|
| A B C | A B C | A B C | A B C | |
| T0 | 0 1 0 | 7 5 3 | 2 3 0 | 7 4 3 |
| T1 | 3 0 2 | 3 2 2 | 0 2 0 | |
| T2 | 3 0 2 | 9 0 2 | 6 0 0 | |
| T3 | 2 1 1 | 2 2 2 | 0 1 1 | |
| T4 | 0 0 2 | 4 3 3 | 4 3 1 |
Example
| Allocated | Max Need | Available | Need | |
|---|---|---|---|---|
| A B C | A B C | A B C | A B C | |
| T0 | 0 1 0 | 7 5 3 | 2 3 0 | 7 4 3 |
| T1 | 3 0 2 | 3 2 2 | 0 2 0 | |
| T2 | 3 0 2 | 9 0 2 | 6 0 0 | |
| T3 | 2 1 1 | 2 2 2 | 0 1 1 | |
| T4 | 0 0 2 | 4 3 3 | 4 3 1 |
Example
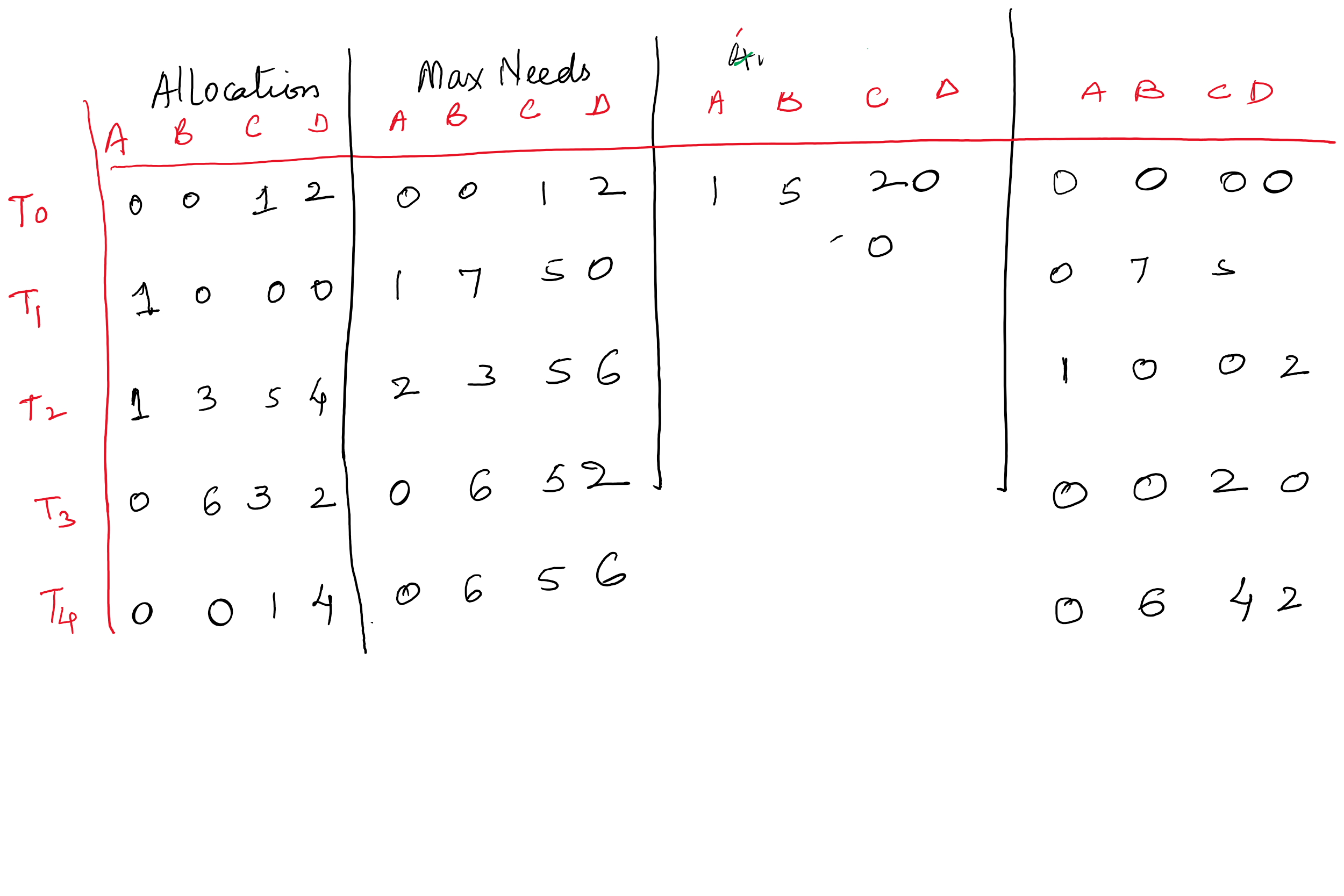
- Can request for (3,3,0) by \(T_4\) be granted?
- No
- Can request for (0,2,0) by \(T_0\) be granted?
- Unsafe state
| Allocated | Max Need | Available | Need | |
|---|---|---|---|---|
| A B C | A B C | A B C | A B C | |
| T0 | 0 3 0 | 7 5 3 | 2 1 0 | 7 4 3 |
| T1 | 3 0 2 | 3 2 2 | 0 2 0 | |
| T2 | 3 0 2 | 9 0 2 | 6 0 0 | |
| T3 | 2 1 1 | 2 2 2 | 0 1 1 | |
| T4 | 0 0 2 | 4 3 3 | 4 3 1 |
Example
Example

Deadlock Detection
- If a system does not employ either a deadlock-prevention or a deadlock-avoidance algorithm, then a deadlock situation may occur. In this environment, the system may provide:
- Allow system to enter deadlock state
- An algorithm to recover from the deadlock
- Recovery scheme
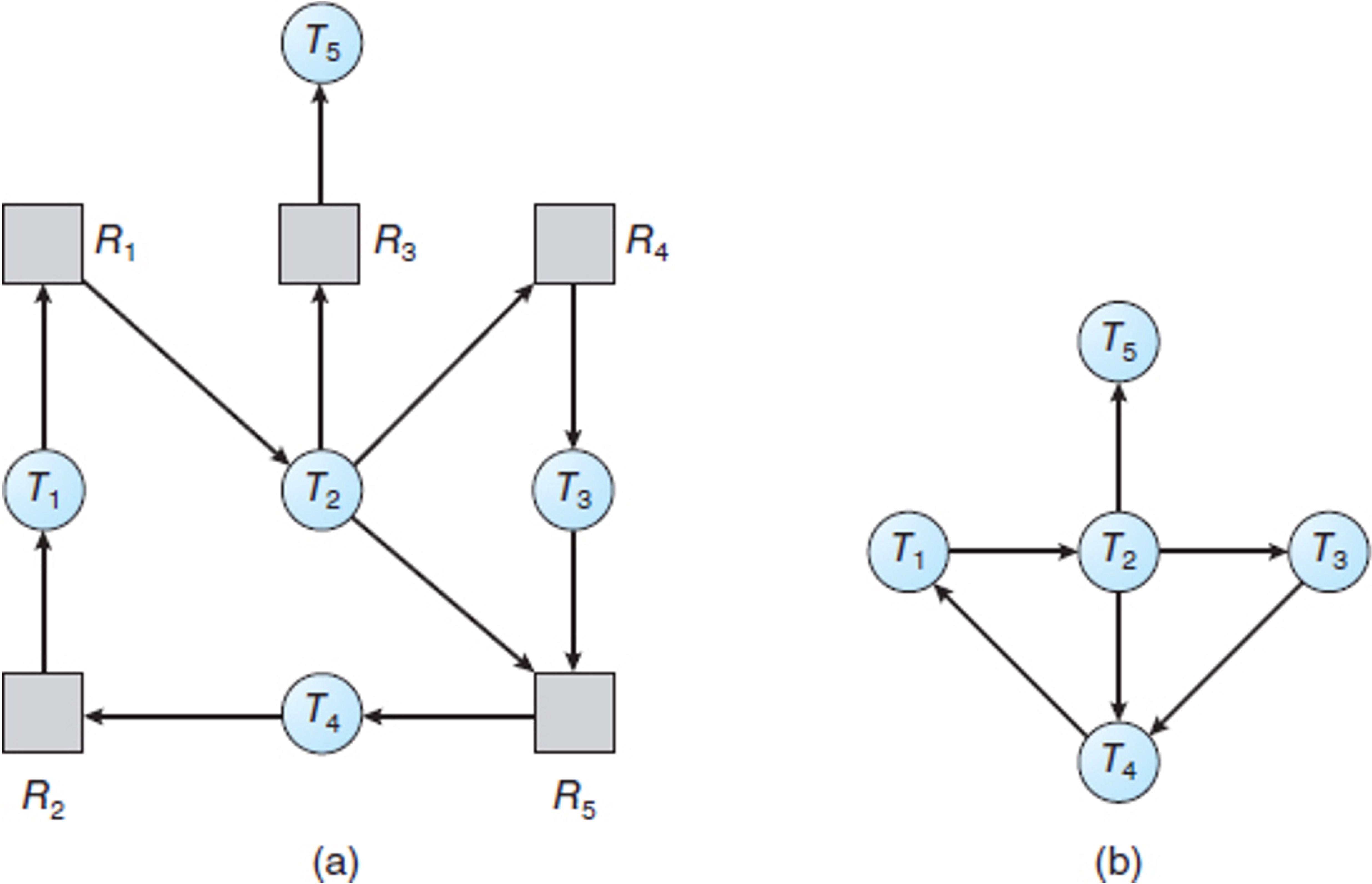
Single Instance of Each Resource Type
- A variant of the resource-allocation graph to m aintain wait-for graph
- Nodes are processes
- an edge from \(T_i\) to \(T_j\) in a wait-for graph implies that thread \(T_i\) is waiting for thread \(T_j\) to release a resource that \(T_i\) needs.
- An edge \(T_i\) \(\rightarrow\) \(T_j\) exists in a wait-for graph if and only if the corresponding resource-allocation graph contains two edges \(T_i\) \(\rightarrow\) \(R_q\) and \(R_q\) \(\rightarrow\) \(T_j\) for some resource \(R_q\) .
- To detect deadlocks, the system needs to maintain the wait-for graph and periodically invoke an algorithm that searches for a cycle in the graph.
- An algorithm to detect a cycle in a graph requires \(O( n^2 )\) operations, where n is the number of vertices in the graph.
Resource-Allocation Graph and Wait-for Graph
Several Instances of a Resource Type
- The algorithm employs several time-varying data structures that are similar to those used in the banker’s algorithm
- Available. A vector of length m indicates the number of available resources of each type.
- Allocation. An \(n × m\) matrix defines the number of resources of each type currently allocated to each thread.
- Request. An \(n × m\) matrix indicates the current request of each thread. If \(Request[ i ][ j ]\) equals \(k\) , then thread \(T_i\) is requesting \(k\) more instances of resource type \(R_j\) .
- To simplify notation, we again treat the rows in the matrices Allocation and Request as vectors; we refer to them as \({Allocation}_i\) and \({Request}_i\) .
- The detection algorithm simply investigates every possible allocation sequence for the threads that remain to be completed.
Detection Algorithm
- Let Work and Finish be vectors of length m and n , respectively. Initialize Work = Available . For i = 0, 1, …, n −1, if Allocation i ≠ 0, then Finish [ i ] = false . Otherwise, Finish [ i ] = true .
- Find an \({index}_i\) such that both
- \(Finish[i] == false\)
- \({Request}_i\) \(≤ Work\) If no such i exists, go to step 4.
- \(Work = Work + {Allocation}_i\) \(Finish[i] = true\) Go to step 2.
- If \(Finish [ i ] == false\) for some \(i, 0 ≤ i < n\), then the system is in a deadlocked state. Moreover, if \(Finish[i] == false\), then thread \(T_i\) is deadlocked.
- This algorithm requires an order of \(m × n^2\) operations to detect whether the system is in a deadlocked state.
Example of Detection Algorithm
- Five processes \(P_0\) through \(P_4\) ; three resource types A (7 instances), B (2 instances), and C (6 instances)
- Snapshot at time \(T_0\) is given and Sequence < \(T_0\) , \(T_2\) , \(T_3\) , \(T_4\) , \(T_1\) > will result in Finish[ i ] = true for all i
| Allocation | Request | Available | |
|---|---|---|---|
| A B C | A B C | A B C | |
| T0 | 0 1 0 | 0 0 0 | 0 0 0 |
| T1 | 2 0 0 | 2 0 2 | |
| T2 | 3 0 3 | 0 0 0 | |
| T3 | 2 1 1 | 1 0 0 | |
| T4 | 0 0 2 | 0 0 2 |
Example (Cont.)
- \(T_2\) requests an additional instance of type C
- State of system?
- Can reclaim resources held by process \(T_0\) , but insufficient resources to fulfill other processes; requests
- Deadlock exists, consisting of processes \(T_1\) , \(T_2\) , \(T_3\) , and \(T_4\)
| Request | |
|---|---|
| A B C | |
| T0 | 0 0 0 |
| T1 | 2 0 2 |
| T2 | 0 0 1 |
| T3 | 1 0 0 |
| T4 | 0 0 2 |
Example (Cont.)

Detection-Algorithm Usage
- When, and how often, to invoke depends on:
- How often a deadlock is likely to occur?
- How many processes will need to be rolled back?
- one for each disjoint cycle
- If deadlocks occur frequently, then the detection algorithm should be invoked frequently.
- Resources allocated to deadlocked threads will be idle until the deadlock can be broken.
- In addition, the number of threads involved in the deadlock cycle may grow.
Detection-Algorithm Usage
- In the extreme, then, we can invoke the deadlock-detection algorithm every time a request for allocation cannot be granted immediately.
- If there are many different resource types, one request may create many cycles in the resource graph, each cycle completed by the most recent request and “caused” by the one identifiable thread.
- Invoking the deadlock-detection algorithm for every resource request will incur considerable overhead in computation time.
Detection-Algorithm Usage
- A less expensive alternative is to invoke the algorithm at set intervals, such as once per hour or whenever CPU utilization drops below 40% percent.
- If the detection algorithm is invoked arbitrarily, it may create many cycles in the resource graph, making it difficult to identify which of the deadlocked processes caused the issue deadlock
Recovery from Deadlock
- When a detection algorithm determines that a deadlock exists, several alternatives are available.
- One possibility is to inform the operator that a deadlock has occurred and to let the operator deal with the deadlock manually.
- Another possibility is to let the system recover from the deadlock automatically.
Recovery from Deadlock: Process Termination
- Abort all deadlocked processes
- Abort one process at a time until the deadlock cycle is eliminated
- In which order should we choose to abort? The question is basically an economic one; we should abort those processes whose termination will incur the minimum cost.
Recovery from Deadlock: Process Termination
- Unfortunately, the term minimum cost is not a precise one.
- Many factors may affect which process is chosen, including:
- What the priority of the process is
- How long the process has computed and how much longer the process will compute before completing its designated task
- How many and what types of resources the process has used (for example, whether the resources are simple to preempt )
- How many more resources the process needs in order to complete
- How many processes will need to be terminated
Recovery from Deadlock: Resource Preemption
- Selecting a victim. As in process termination, we must determine the order of preemption to minimize cost. Cost factors may include such parameters as the number of resources a deadlocked process is holding and the amount of time the process has thus far consumed.
- Rollback. Clearly, it cannot continue with its normal execution; it is missing some needed resource. We must roll back the process to some safe state and restart it from that state.
Recovery from Deadlock: Resource Preemption
- Starvation. How do we ensure that starvation will not occur? That is, how can we guarantee that resources will not always be preempted from the same process?
- In a system where victim selection is based primarily on cost factors, it may happen that the same process is always picked as a victim.
- As a result, this process never completes its designated task, a starvation situation any practical system must address.
- Clearly, we must ensure that a process can be picked as a victim only a (small) finite number of times.
- The most common solution is to include the number of rollbacks in the cost factor.
References
- A. Silberschatz, P.B. Galvin, and G. Gagne. Operating System Concepts , 10th Edition; 2018; John Wiley and Sons.